※ 이 게시글은 6월 1일 작성 되었습니다. (원본 링크)
지난 강의 보충
벡터의 뺄셈
마이너스 벡터를 덧셈하는 것과 같다.
교환 법칙이 성립하지 않아서 빼는 순서에 의해 방향이 달라진다.
12강
동차 좌표

2D공간과 3D공간과의 크기를 제어하는 행렬은 대각선에 있다.
평행 이동을 하는 위치 변환을 기존 행렬의 곱셈 규칙에 적용하기 위해서는
새로운 축이 더 필요하다.
이것을 동차 좌표라고 한다.
왜 하나의 축이 더 추가되었을까?
그것은 이동을 위해서 추가된 것이라고 말할 수 있다.
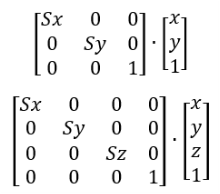
동차 좌표를 적용한 크기 행렬의 곱셈
행렬의 곱셈을 이용한 이동 행렬

벡터는 원점에서 뻗어 나가는 벡터의 개념과 충돌된다.
가상의 차원을 늘려서 밀기 변환하고 남는 차원은 버린다.
좌표에 이동 값을 더하면 쉽게 이동이 가능하다.
직접 행렬을 곱해 보면 (x+dx, y+dy, z+dz, 1) 이라는 결과가 나오게 된다.
(마지막 1은 사용하지 않고 버리면 됨)
회전 변환과 회전 행렬

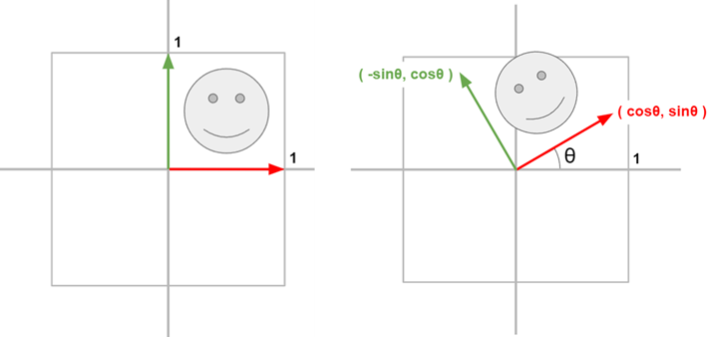
기저 벡터가 회전함으로서 기준이 되는 백토 공간이 회전된다.
그럼으로 공간 전체가 움직인다.
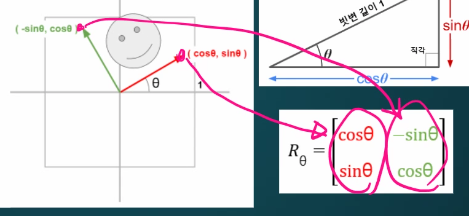
식으로 나타내면 이렇다.
변환의 결합
변환 행렬의 가장 큰 장점은 행렬을 결합할 수 있다는 것이다.
행렬을 크게 세가지로 분류할 수 있다.
이동 행렬 M
회전 행렬 R
크기 행렬 S
이동 행렬 M과 회전 행렬인 R, 크기 행렬 S가
이동과 회전 후 크기를 바꾸는 행렬의 곱셈 S∙R∙M을 계산해
그 행렬을 T라고 하면
T는 이동, 회전, 크기 변환 모두를 수행할 수 있는 복합 행렬이 되는 셈이다.
이 과정을 변환의 결합 이라고 한다.
3D Max 스크립트 활용하기
맥스 스크립트를 여는 방법 <Scripting - Open Script>
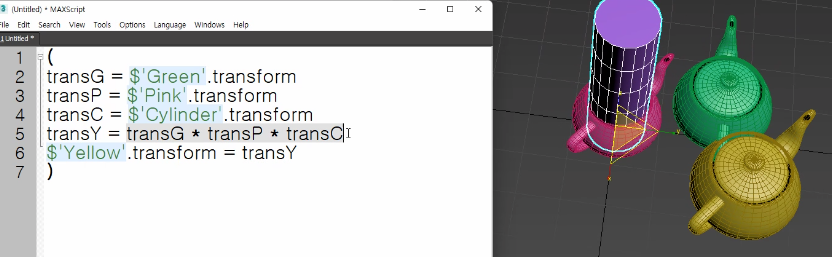
위 사진을 보자. 여기서 $는 오브젝트의 이름을 표기하기 위해서 필요하다.
이 때 이름에는 공백이 없어야 한다. 공백 갯수를 기준으로 계산을 여러번 하게 될 수 있기 때문이다.
초록색 주전자의 위치를 transG,
분홍색 주전자의 위치를 transP,
보라색 원기둥(실린더)의 위치를 transC,
노란색 주전자의 위치를 transY라고 할 때
노란색 주전자의 위치는 위의 세개의 오브젝트의 위치 값을 계산한 값이라고 하고
transY = transG * transP * transC
이 세개의 위치(행렬)을 곱한 값이 노란색 주전자가 됨으로
노란색 주전자는 결과적으로 이동, 회전, 스케일 값을 모두 가지고 있으며
하나의 새 행렬이 되는 것이다.
x, y, z 세개의 축에 대한 오일러 회전 (3차원 회전)
Roll은 z축 중심 회전이고 x, y 평면 회전이다.

Pitch는 x축 중심 회전이고 y, z 평면 회전이다.
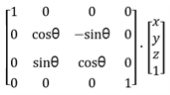
Yaw는 y축 중심 회전이고 x, z 평면 회전이다.

오일러(Euler) 회전의 순서
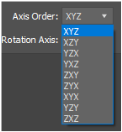
3D Max나 Maya를 자주 접해 봤으면 오브젝트를 Euler로 제어할 때 보던
'Axis Oder'가 떠오를 것이다.
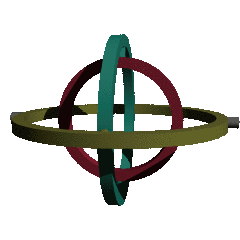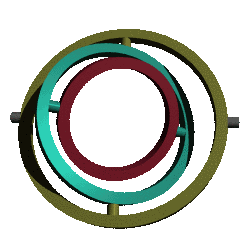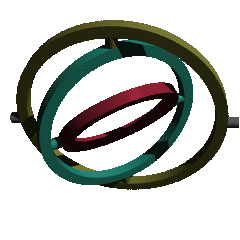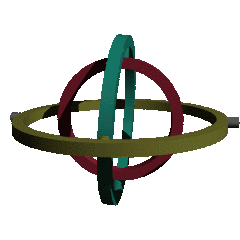
3차원인 공간의 회전은 각 축의 회전 행렬을 원하는 순서대로 곱해서 만들어지게 된다.
x, y, z 어느 축을 먼저 돌리냐에 따라서 순서가 달라진다.
회전하는 축 3개의 각도를 순서를 정하고, 회전하여 자세를 나타내는 것이 오일러 각이다.
역행렬
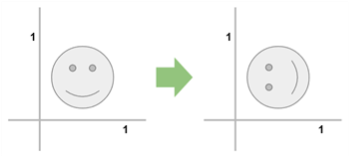
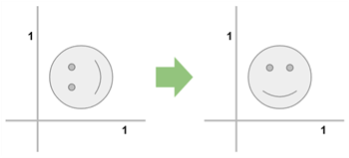
역행렬을 만드는 과정은 이동, 회전, 크기 변환에 각각 다르게 계산해야 한다.
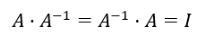
역행렬은 -1 첨자를 사용하여 표기한다.
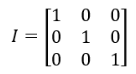
특징이 하나 있다면 행렬과 역행렬을 곱하면 항등 행렬이 된다는 것이다.
벡터의 MVP변환
중요하게 알아야 하는 것
- 행렬을 곱하는 순서의 중요성
- 결합 행렬 시연
좌표 공간의 종류
View → Projection 변환 = Clip Space
화면 밖은 클리핑해서 잘라낸다.
뷰공간에서 프로젝션 변환을 했을 경우에는
결과적으로는 버텍스의 값이 변경된다. (시각화)
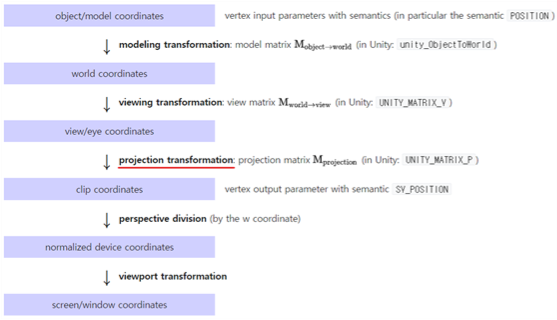
Vertex Transformations (참고자료 출처)
버텍스 셰이더에서 출력하는 최종 결과물은 Projection 좌표계이다.
공간 변환 함수를 사용하는 이유는 무엇일까?
그전에 여러 단계의 공간 변환을 거치는 이유는
사실 한번에 최종 변환으로 가도 문제는 없다.
하지만 작업을 하다 보면 다양한 목적의 셰이더 코드를 만들게 되는데
가끔 각각의 공간 좌표계가 필요할 때가 있기 때문이다.
mul(UNITY_MATRIX_MVP, positionOS)
UnityObjectToClipPos(positionOS)
이 두개의 함수는 같지만 다르다.
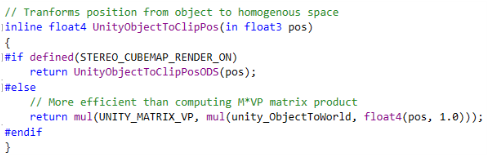
URP 함수인 TransformObjectToHClip은 별 다른 기능 없이
단지 더 효과적이라고만 설명되어 있다.
클립 공간(Clip Space)

- URP 셰이더의 positionHCS.z
positionHCS.z 값 : Camera의 Far ~ Near를 기준으로 0 ~ 1
View 공간의 x와 y값과는 미묘하게 다르다. 화면의 종횡비에 영향을 받는다.
(Vew 공간의 x와 y는 카메라 종횡비와 무관하다)
카메라에서의 안보이는 부분을 잘라내기 때문에 절단 공간으로도 불린다.
정규 기기 공간(Normalized Device Coordinates)

NDC 공간은 화면 가로 세로 비율과 무관하다.
(가로의 경우) OUT.positionHCS.x / OUT.positionHCS.w → -1 ~ 1
스크린 공간 (Screen Space)
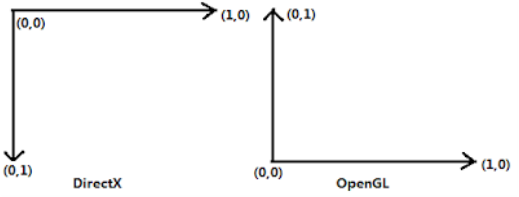
0~1의 UV 공간이며,
OpenGL과 DirectX의 방향이 다르다
mul 함수
mul 함수는 거의 대부분 데이터형을 인수로 받고 있다.
'교내 활동 > 게임그래픽엔진심화' 카테고리의 다른 글
| 게임그래픽엔진심화 14강 - 샘플러, UV 회전, Diffuse Wrap, 굴절, 반사, Normal Map (1) | 2022.09.30 |
|---|---|
| 게임그래픽엔진심화 13강 - 아웃라인 셰이더, BRDF, Lambert, Half Lamb···, Blinn Phong, Fresnel, 버텍스 라이팅, IBL, SH, Blending (2) | 2022.09.30 |
| 게임그래픽엔진심화 11강 - 벡터, 기저벡터와 변환, 행렬 (1) | 2022.09.30 |
| 게임그래픽엔진심화 10강 - 함수와 구조체, 시멘틱, 전처리, 네이밍 관례, if분기, 좌표계 (1) | 2022.09.30 |
| 게임그래픽엔진심화 9강 - ShaderLab, 함수와 구조체 (1) | 2022.09.30 |


