※ 이 게시글은 5월 25일 작성 되었습니다. (원본 링크)
벡터(Vector)
벡터
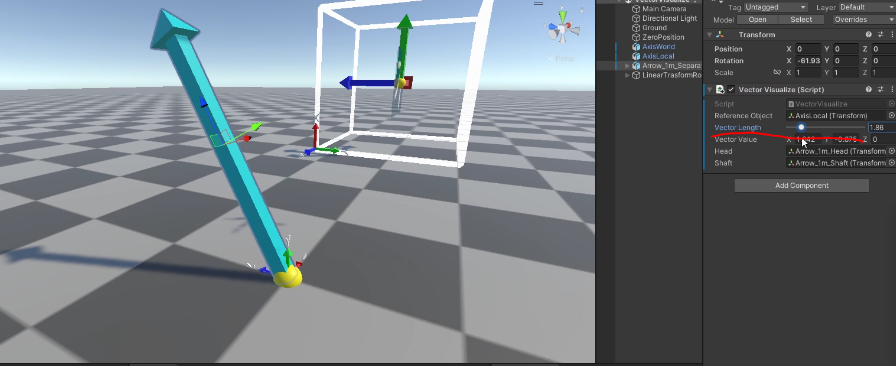
공간에 떠있는 입체 화살표이다.
2차원과 3차원 공간 좌표.
유니티 화면 오른쪽에 보면 이런식으로 길이값을 조정해 시각화할 수 있다.
일종의 방향 정보이며,
렘버트라이팅 연산을 하기 위해서도 필요하다.
방향 벡터 구할 때도 사용된다.
때로는 공중에 떠 있기도 한다.
하지만 그럼에도 원점을 기준으로 하는 것은 동일하다.
스칼라 - 각각의 숫자, 거리
램버트, 아웃라인
벡터의 덧셈
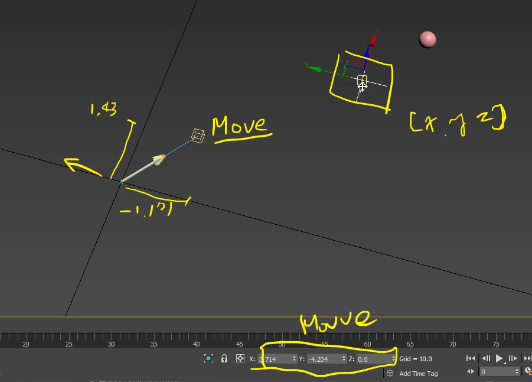
벡터의 덧셈은 어느 위치에 있든 상관없이 값을 더해주면 된다.
사진을 봐보자.
무브라고 되어 있는 곳을 보면, 바라보는 방향(더해주는 값)이 현재 빨간공이고
그것이 곧 원점에서부터 네모 체크박스까지의 위치가 된다.
중요한 개념
- 노말라이즈(normalize)
- 단위 벡터
정규화된 벡터는
아무리 길이가 길든 짧든 정규화된 벡터의 크기는 그대로다.
벡터의 뺄셈
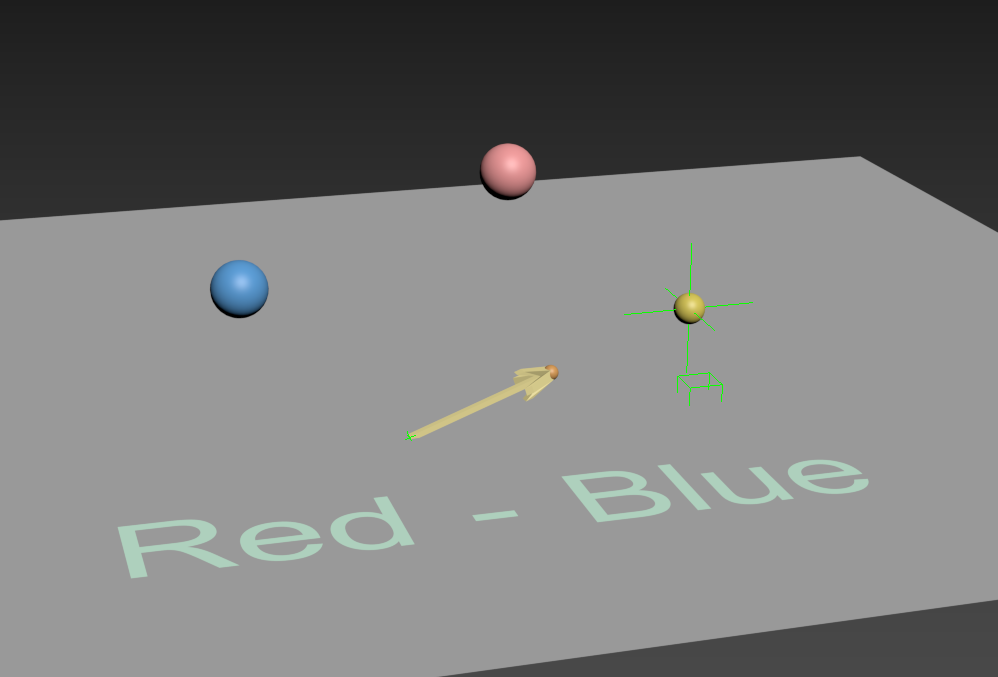
공중에서 파란 오브젝트가 바라보는 방향(빨간 공)이 곧 원점에서부터 노란공 까지의 거리와 같다.
(빨간공 좌표 빼기 파란공 좌표는 노란색 공(벡터)이다.
2D 평면에서 봐보자.
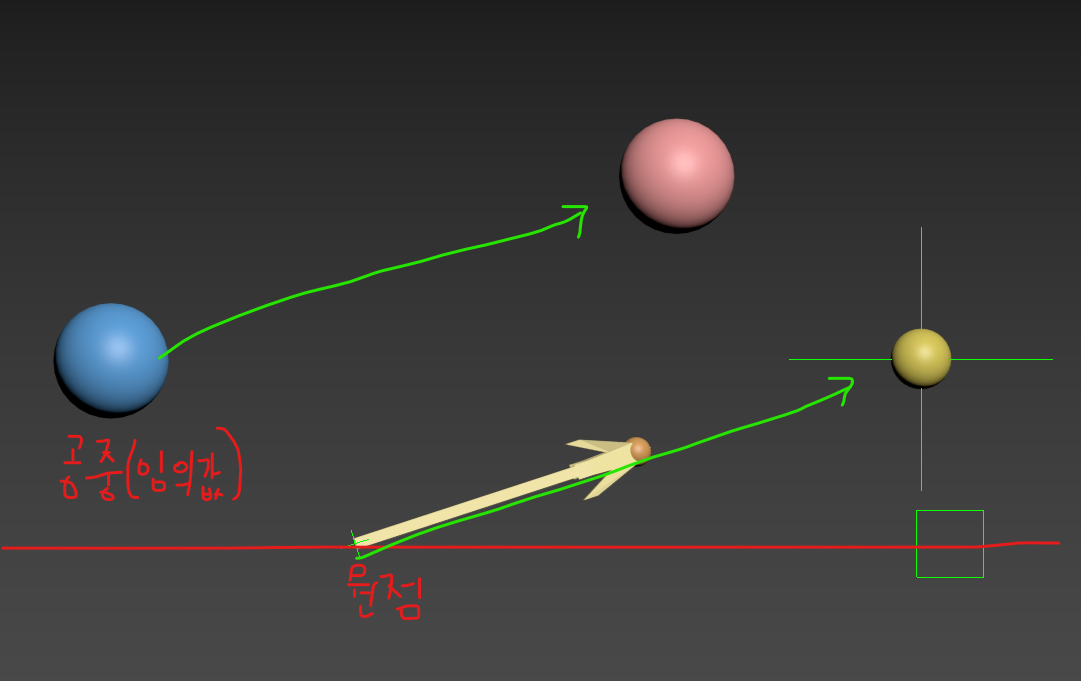
즉 오브젝트가 바라보는 방향이 된다.
뺀 결과는 항상 원점에서부터 시작 된다.
그리고 빨간공에서 노란공까지의 거리를 빼보면, 파란공이 된다.
바라보는 방향이 반대가 되어도 길이는 같기 때문에 항상 뺄셈을 하기 전에 순서에 신경써서 할 필요가 있다.
벡터의 내적
두개의 벡터를 수직 투영시켜 밑변의 길이를 알아낸다.
가장 기본이 되는 방식이다.
벡터의 외적
두개의 벡터와 벡터를 받아들인다.
주로 노말벡터에 사용된다. (노말맵 사용할 때)
행렬

행렬은 수 등을 행(row)과 열(column)로 맞춰서 직사각형 모양으로 보기 쉽고 순서에 맞게 배열한 것이다.
mul 함수
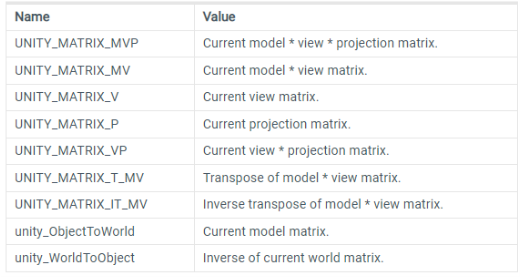
기본으로 제공하는 행렬 변수들.
공간의 위치가 되는 어떤 특정 좌표가 존재할 때 이 함수를 사용하여
그 위치를 지정한 행렬로 공간을 변환해 새로운 위치 값을 지정한다.(반환)
렌더파이프라인에서 기본으로 제공하는 행렬 변수들을 주로 가져다가 쓴다.
행렬의 구조, 행(row)과 열(column)
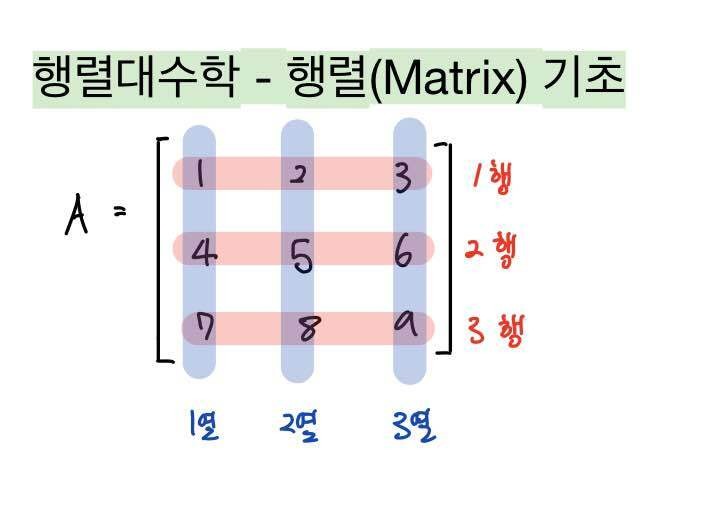
빨간색 가로 줄이 행, 파란색 세로 줄이 열이다.
각각 행은 m, 열은 n으로, 이 행렬의 크기는 (m x n) 이 된다.
그러므로 위와 같은 경우는 3 x 3 행렬이 된다.
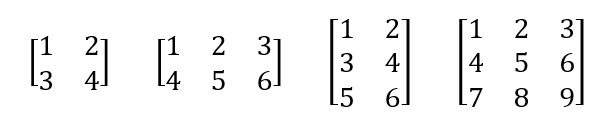
위 그림은 왼쪽부터 순서대로 (2 x 2), (2 x 3), (3 x 2), (3 x 3) 행렬이 된다.
간단히 말해서 숫자를 가로세로 구조로 배열해 놓은 것. 마치 바둑판같이 되어 있다.
행렬의 용어
정방 행렬 = 가로 세로의 크기가 같은 행렬.
가로세로 크기가 5X5면 5차 정반 행렬이 된다.
행동 행렬, 단위행렬 - 정방 행렬이지만 대각선으로 성분이 모두 1로 통일된다.
영 행렬 - 모든 원소가 0임.
전치 행렬 - 행과 열을 서로 교환해서 얻는다. 위 첨자 T를 표시한다.
행렬의 곱셈
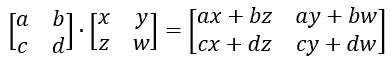
행렬의 곱셈은 본격적인 공간의 변환이다.
다만 행렬의 스칼라 곱과는 다르다.
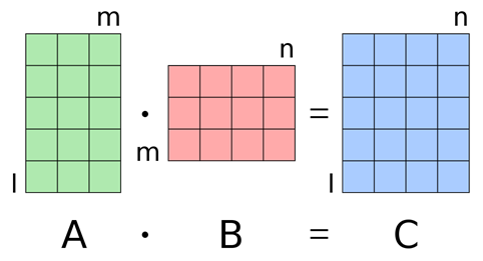
행렬의 곱셈을 하기 위해서는 첫번째 행렬의 열 갯수와, 두번째 행렬의 행 갯수가 동일해야 한다.
위 그림으로 보면, 초록색 A의 열은 3, 빨간색 B의 행도 3이므로 동일한 것을 알 수 있다.
행렬의 곱셈 - 교환법칙, 결합 법칙
A*B =/ B*A
(A-B*C = A*(B*C)
행렬에서는 순서가 중요하다.
벡터 평면, 벡터 공간
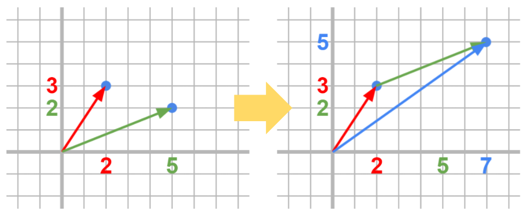
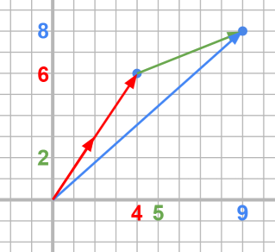
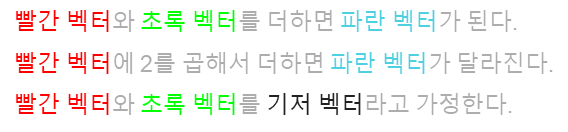
그렇다.
기저벡터에 무수히 많은 값을 곱하게 되면 그만큼 무수히 많은
위치를 얻는다.
이것을 벡터 평면이라고 부른다.
여기서 Z축 벡터가 더해지면 벡터 공간이 된다.
표준 기저 벡터
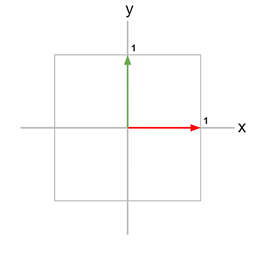
기저 벡터는 무수히 많이 존재할 수 있다.
기저벡터 중에서도 0과 1로 이루어진 기저벡터를
표준 기저 벡터로 불린다.
가로 방향이 (1, 0), 세로 방향이 (0, 1)
이 기저벡터의 평면에 있는 임의의 벡터는 밑 그림과 같이 표현할 수 있다.
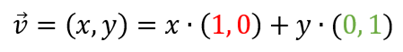
표준 기저 벡터의 변환
좀 더 심화해서 들어가보면,
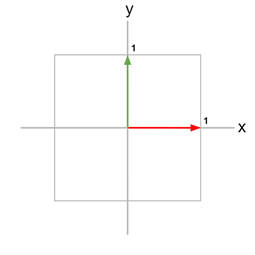

앞선 내용에서는 표준 기저 벡터의 평면은 이런식으로 나와있다.
그런데 이 벡터가 변형되면
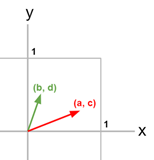
이런 식으로 나오게 된다.
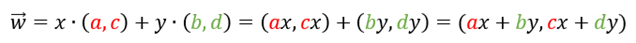
이것은 행렬의 곱셈 연산인데 매우 복잡하게 생겼다.
자세히 살펴보면 기저벡터는 열 백터로 구성되어 있다는 것을 알 수 있다.
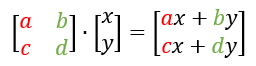
그리고 이것을 변환 행렬이라고 부른다.
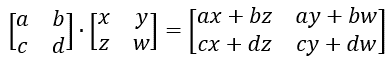
이것은 행렬의 곱셈이다. 지금와서 보면 위와 비슷한 식임을 알 수 있다.
표준 기저 벡터에 의한 크기의 변환
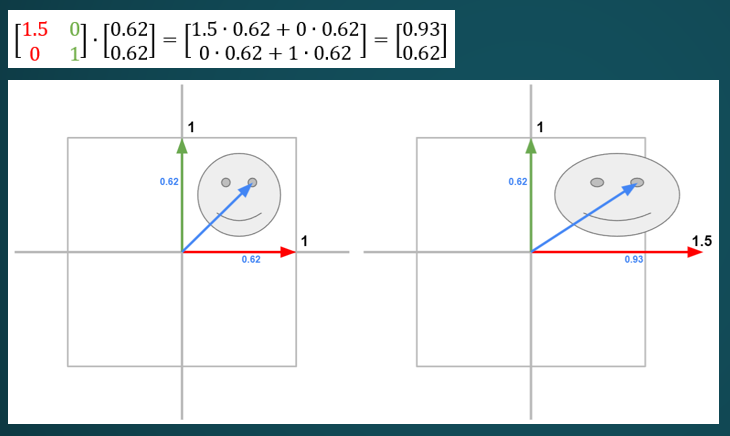
결과적으로 위의 두 식을 이용하여 위 이미지의 크기가 달라졌음을 알 수 있다.
'교내 활동 > 게임그래픽엔진심화' 카테고리의 다른 글
| 게임그래픽엔진심화 13강 - 아웃라인 셰이더, BRDF, Lambert, Half Lamb···, Blinn Phong, Fresnel, 버텍스 라이팅, IBL, SH, Blending (2) | 2022.09.30 |
|---|---|
| 게임그래픽엔진심화 12강 - 행렬, MVP 변환과 아웃라인 셰이더 (0) | 2022.09.30 |
| 게임그래픽엔진심화 10강 - 함수와 구조체, 시멘틱, 전처리, 네이밍 관례, if분기, 좌표계 (1) | 2022.09.30 |
| 게임그래픽엔진심화 9강 - ShaderLab, 함수와 구조체 (1) | 2022.09.30 |
| 게임그래픽엔진심화 8강 - Lambert 셰이더 맛보기, ShaderLab (1) | 2022.09.30 |